- September 19, 2019
- Posted by: fyber
- Category: programming language
When we develop any application, we need to store application data. We can store application data by using a linear and non-linear data structure. But the problem is how to search any element in a given data-set and which data searching method is best for any specific data-set. To solve this problem, we should have a good knowledge of data structure.
However, there are many data searching techniques available. But we are going to discuss the binary search. which is faster than a linear search algorithm?
What is a binary search?
Binary search is a technique of finding the required data from an array. It is a very fast and efficient searching technique compared to a linear search. Point to remember that we can implement binary search only on a sorted array.
How Binary Search Work
Binary search divides the large problem into a small problem. First, it divides the list into the two-part as an interval. Compared to the required data from the middle value.
If the middle value is equal to the required data, then the binary search will terminate the process and it will print the required element.
If not found, then it will check that the required data is less than the middle value or greater than middle value. however, If middle value is greater than required value, the searching process will continue on the left side of the middle value. Otherwise, it will search the right side of the middle value.
Pre-requirement to implement binary search
-
- Sorted list.
- Number of steps to find Required data.
1. Sorted list.
For example, we have an unsorted array below and we want to find element 42 in the array list. Then we have to sort this list in any order either ascending or descending. Because binary search can implement only on a sorted array.
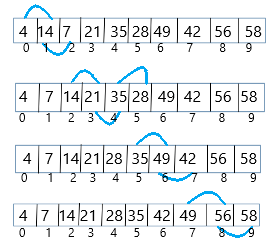
Sorting means arrange list into either ascending or descending order. Let’s first try to sort this array in increasing order. Algorithm to sort an array
Algorithm to sort an array
|
Let’s solve this algorithm.
- Compare 4 to 14, no need to swap because 4 is smaller than 14.
- After that compare 14 to 7 and swap because 7 is smaller than 14.
- Now compare 14 to 21, no need to swap because 14 is smaller than 21, and compare 21 to 35 no need to swap.
- Again compare 35 to 28 and swap because 28 is smaller than 35.
- Then compare 35 to 49, no need to swap so compare 49 to 42 and swap.
- Repeat comparison 49 to 56, no need to swap again compare 56 to 58, no need to swap.
See the below image;
Finally, we have a sorted list, see the below image;
Before implementing a binary search on this list we should know the time complexity of the binary search. Which we illustrate below.
you can also learn about Java vs C# programming language.
Time complexity of the binary search
Time complexity means that how much steps will spend to retrieve data from a list, is called time complexity. We can calculate the time complexity of binary search by the formula.
The formula for binary search time complexity is Olog(n). But actually we can abbreviate Olog(n) as log2(n) because the base of the log doesn’t matter. So first see illustrate how log2n works.
Expression: log2(n)
| – – – – – – – – – – – – – – – For n = 2: log2(21) = 1 Output = 1 – – – – – – – – – – – – – – – For n = 4 log2(22) = 2 Output = 2 – – – – – – – – – – – – – – – For n = 8 log2(23) = 3 Output = 3 – – – – – – – – – – – – – – – For n = 10 log2(25) = 5 Output = 5 |
Now you have understood how Olog(n) works so we can examine how many steps we require for searching required data. let’s see.
2. Number of steps to find Required data.
As we have 10 elements in our array. If value not found after the first iteration, Binary search will divide the array into half, and leaving behind 5 element then 2 elements after the second execution.
Likewise, in last only 1 element will remain, which will either match to the required value or not. For checking this value will require one more step and we will add one more step. So finally binary search will need 5 steps to find required value,
Because n=10 =log2(25) = 5.
Steps to find data from the list by using binary search
Binary search works on the principle of divide the large problem into a different small problem and for doing this process we have a formula for mid-value = L+(R-L)/2. Where L is a left lower memory address and R is a right side higher memory address.
Let’s see how we have implemented this formula in our example.
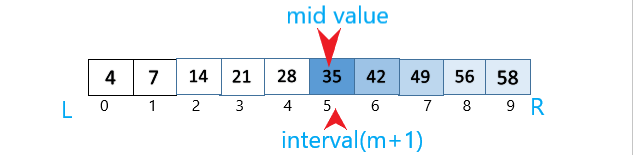
- Step 1. 0+(9-0)/2= 9/2=4.5
Because we use integer part only so the mid part will be 4. And add 1 to mid value 4+1=5. Thus mid-value is =35.
- Step 2: So, list [35] <42 and not equal to list [35]. So we will search to the right side of mid-value.
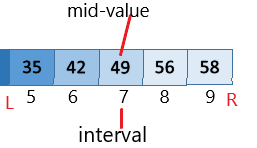
- Step 3. Now L= 5 and R= 58
5+(9-5)/2=14/2=7
- Step:4 Now list [49] >42 and not equal to mid-value then we will search to the right side of mid-value till starting point.
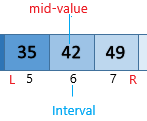
- Step 5: Now L=35 and R= 49.
So, 5+(7-5)/2=12/2=6
- Now mid-value is equal to the required data at 6th location. So it binary search will print this value.
You can also read click here.
Binary search algorithm
We hope you understand how binary search works. Now it’s time to write an algorithm for binary search. you can implement this algorithm in any programming language.
|
You can also read our article advantage of C#.
Summary
Binary search has reduced time to find data in an array. There are various methods for searching and sorting in the data structure. These methods we can implement according to data’s nature. The algorithm which we described above, you can implement on any programming language, like Java programming, C# programming, and C++ programming language.